CORREAS
Indice:
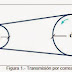
Las correas se utilizan para transmitir, mediante un movimiento de rotación, potencia entre árboles normalmente paralelos, entre los cuales no es preciso mantener una relación de transmisión exacta y constante.
El hecho de no poder exigir una relación de transmisión exacta y constante se debe a que en estas transmisiones hay pérdidas debido al deslizamiento de las correas sobre las poleas. Dicho deslizamiento no es constante sino que varía en función de las condiciones de trabajo, es decir, de los valores de par transmitido y de la velocidad de la correa.
Las transmisiones por medio de correas son denominadas de tipo flexible pues absorben vibraciones y choques de los que sólo tienden a transmitir un mínimo al eje arrastrado.
Son estas transmisiones adecuadas para distancias entre ejes relativamente grandes, actuando bajo condiciones adversas de trabajo (polvo, humedad, calor, etc.), son además silenciosas y tienen una larga vida útil sin averías ni problemas de funcionamiento.
CORREAS PLANAS. CARACTERÍSTICAS Y CÁLCULO
Las correas del tipo plano están constituidas por una banda continua cuya sección transversal
es rectangular, fabricadas de distintos materiales siendo los más empleados:
• Cuero de 4 a 6 mm. de espesor. Para bandas de más espesor se unen capas sucesivas de
cuero mediante adhesivos, construyéndose bandas de dos capas y bandas de tres capas.
Según su capacidad se pueden clasificar en tres grupos:
- Clase I:
σpermisible = 25 Kp/cm2 y velocidad máxima de hasta 12 m/s.
- Clase II:
σpermisible = 29 Kp/cm2 y velocidad máxima de hasta 24 m/s.
- Clase III:
σpermisible = 33 Kp/cm2 y velocidad máxima de hasta 45 m/s.
• Tejido de algodón o banda de nylon. Se construye con varias capas de tejido, normalmente recubiertas de caucho o plástico para su protección y mayor duración.
Su tensión permisible varía entre los 125 y 250 Kg/cm2 y su velocidad lineal máxima es de hasta unos 40 m/sg.
Hay un concepto muy utilizado en las transmisiones por correa, es el de relación de transmisión.
Sea d1 el diámetro de la polea motriz y d2 el de la polea arrastrada:
Es evidente que por ser la correa una banda continua la velocidad lineal en cualquiera de sus puntos tiene el mismo módulo. Por tanto si V es la velocidad lineal se cumplirá (despreciando el deslizamiento) que:
V =ω1⋅ r1 =ω 2 ⋅ r2
Como:
ω1⋅ r1 =ω 2 ⋅ r2
Se tiene que:
n ⋅d = n ⋅d ⇒(d1/d2)=(n2/n1)
La relación:
d1 diametro polea motriz
r= ________ = _______________________
d2 diametro polea arrastrada
se denomina relación de transmisión.
Si se considera un elemento de correa, como se presenta en la figura siguiente, de longitud dL se tiene que:
Si T es la fuerza que debido a la tensión de la correa tiende a unir las dos poleas, debido al giro de la polea en un ramal de la correa habrá una fuerza F1 mayor que la fuerza resultante en el otro ramal F2.
F1 - F2 es la diferencia entre el ramal cargado y descargado.
Vamos a demostrar que:
(F1/F2) = e^(μθ)
Siendo:
μ = coeficiente de rozamiento correa-polea
θ = ángulo de contacto correa-polea
Si dN es la fuerza que actúa entre la correa y la polea y dS es la fuerza centrífuga del elemento de correa considerado, se tendrá que como la fuerza resultante normal es cero:
ΣFn = 0 ⇒ 0 = dN+ dS - F sen (dθ/2) - (F + dF)sen (dθ/2)
Como dθ es muy pequeño ⇒ sen (dθ/2) = dθ/2
0 = dN+dS- F • (dθ/2) - F +dF • (dθ/2)
Despreciando: dF ⋅ dθ/2
Se tiene:
0 = dN+dS-F⋅d θ ⇒ d N = F.d θ - d S
Si se supone que no hay deslizamiento de la correa sobre la polea, se tiene que:
ΣFt = 0
0 = μdN+F cos (dθ/2) - (F + d F) cos (dθ/2)
Siendo:
μ = coeficiente de rozamiento correa-polea.
Como dθ es pequeño ⇒ cos (dθ/2) → 1 por lo que:
0 = μ ⋅d N- d F
Como: dN = F dθ - dS
0 = μ (F⋅d θ - dS) - dF
o bien:
0 = μ ⋅F⋅ d θ - μ ⋅ dS - dF
Si la masa del elemento dL de correa es dm, si V es la velocidad lineal de la correa se tiene que:
dS = dm.(V^2/R)
Si γ es el peso específico de la correa:
dm = b.h.dL.γ
Siendo
b = anchura de la correa
h = espesor de la correa
Como:
dL=( R+(h/2) ) * dθ ~ = R*dθ
Siendo
R = radio de la polea
Se tiene que: dm = b.h.γ .R.d θ
Con lo que:
Ecuación que será de gran utilidad en el cálculo de frenos.
De forma inexacta, como los valores de K son pequeños, es frecuente encontrar en el cálculo de transmisiones por correa la fórmula (I) obtenida anteriormente.
El coeficiente de rozamiento μ entre polea y correa está muy estudiado, habiendo tablas como
la) siguiente que ofrecen valores de μ.
En el caso del cuero sobre poleas de acero hay una fórmula empírica que ofrece el valor de μ
ligado a la velocidad lineal de la correa.
μ = 0'22 + 0'012.V
Siendo V = velocidad lineal de la correa en m/s
Un aspecto necesario para el uso de las transmisiones por correa es el del cálculo de la longitud de la correa en función de los diámetros de la polea motriz y arrastrada.
Para ello usando el esquema de la figura siguiente se tiene:
De la figura se obtiene que:
l = O1O2.cos α
Siendo:
O1 O2 = distancia entre centros de las poleas
L = AB+BC+CD+DA
AB = CD = l = O1 O2 cosα
AD = r ( π - 2α ) ; BC = ( π + 2α ) R
R - r
sen = _______
O1 O2
R - r
α = arcsen ________
O1 O2
L =π r - 2r α + π R + 2R α + 2O1O2cos α
L = π (R + r) + 2 α (R - r) + 2O1O2cos α
El cálculo de la sección transversal de la correa se calcula con la fórmula que ofrece la tensión o esfuerzo en el ramal más cargado, o sea el sometido a la carga F1:
σ= (F1/A)
Como σ ≤ σpermisible ⇒ Área mínima de la sección vendrá dada por:
A = F1/σpermisible
Como el área A es una sección rectangular, si b es la anchura de la correa se tendrá que el espesor mínimo necesario en la correa es a, dado por:
a.b = A ⇒a=A/b
La velocidad de la correa, como se desprende del estudio realizado, incide de manera notable en su comportamiento, ya que la fuerza centrífuga crece rápidamente con la velocidad y puede llegar a valores a los que la capacidad de transmisión de potencia se anula. En la práctica no se aconsejan velocidades mayores de 30 m/s, ya que las flexiones a las que se somete la correa al pasar sobre las poleas actúan sobre la vida útil y a más velocidad lineal mayor es el número de flexiones a las que se somete la correa por unidad de tiempo y menor, lógicamente, será su vida útil. Un aspecto de gran importancia en el cálculo de transmisiones con correas planas es el del diámetro mínimo aconsejable de poleas. Esta es una medida empírica cuyos valores usuales son los siguientes:
Para poder transmitir potencia la correa debe tener una tracción inicial, la denominada tracción de reposo. Se recomiendan unos 125 N/cm de anchura de correa. Cuanto más tensa esté la correa más potencia se puede transmitir sin deslizamiento excesivo, pero por contra mayor y más rápido es el deterioro. Como ocurre que con el servicio las correas se alargan haciéndose necesario el tensado periódico, se recurre a sistemas de ajuste bien por basculamiento bien por desplazamiento o bien, y esta es una solución muy racional, por polea de tensión que no sólo permite regular la tensión sino que posibilita un mayor contacto de la correa con la polea.
CORREAS TRAPECIALES. CARACTERÍSTICAS Y CÁLCULO
Las correas trapeciales o en V son las más ampliamente usadas en este tipo de transmisiones. Se construyen de caucho en cuyo interior se colocan elementos resistentes a la tracción. El esquema de una correa es el siguiente:
Los componentes que forman una correa trapecial son:
- A: Funda exterior de tejido vulcanizado
- B: Elementos que soportan la carga
- C: Cojín resistente de caucho
- D: Capa de flexión
Las poleas con garganta acanalada afectan a la capacidad de transmisión ya que el denominado efecto cuña da lugar a una fuerza normal de la correa sobre la polea muy superior a la de las correas planas.
El efecto cuña favorece también el uso de correas aplicadas a poleas con reducida distancia entre sus centros, y grandes diferencias entre los diámetros.
Es frecuente encontrar transmisiones con correas trapeciales múltiples, con la única condición de que se usen correas especialmente próximas en longitud, es decir, de estrecha tolerancia en su fabricación, pues, en caso contrario, la correa más corta trabaja en exceso y se romperá demasiado pronto.
( (F1-k) / (F2-k) ) = e^(μθ)
obtenida para correas planas es igualmente útil si se sustituye μ por μ/sen φ, siendo 2 φ el ángulo de la garganta que es próximo a 35º.
Para determinar la relación de transmisión es preciso definir el diámetro primitivo dp, que es el que corresponde en la polea a la fibra neutra de la correa. Se denomina fibra neutra a aquella fibra cuya longitud no cambia cuando la correa se dobla perpendicularmente a su base.
La relación de transmisión de las transmisiones en correas trapeciales viene dada por:
dp1 ⋅ n1 = dp2 ⋅ n2
Las correas trapeciales, en función de sus dimensiones, se agrupan según la norma UNE
18006-93 en siete tipos básicos según su sección transversal, a saber, Y, Z, A, B, C, D y E.
En la tabla siguiente se presentan los valores característicos de los siete tipos de correas comerciales:
Además de las dimensiones señaladas para cada tipo de sección, la norma UNE 18006-93 indica los desarrollo primitivos y las tolerancias de fabricación, aspecto este último de suma importancia para lograr un trabajo correcto en las transmisiones de correas múltiples.
En referencia a los aspectos más importantes de la poleas de garganta para correas trapeciales estan recogidos en la norma UNE 18164-88.
Los ángulos de garganta que se utilizan para la construcción de éstas son ligeramente inferiores a los ángulos de los flancos de la correas que van a alojar, en concreto se fabrican poleas con valores de 32º, 34º, 36º y 38º.
El esquema de una polea con acanaladuras trapeciales es el que se presenta en la figura siguiente:
Las dimensiones de poleas según la Norma UNE 18164-85 son las que se presentan en la tabla siguiente:
Igualmente se establecen un número de diámetros de referencia limitados para cada tipo de sección de garganta, estableciendose unos valores recomendados (para las condiciones medias de funcionamiento) y unos valores mínimos, que se indican en la siguiente tabla:
Existe mucha más normativa referida a las correas trapeciales que la citada y que abarca aspectos tales como las tolerancias de fabricación y montaje de los elementos de una transmisión, las comprobaciones que se deben realizar sobre cada uno de los componentes, tipos especiales de correas trapeciales y otros muchos aspectos.
El uso de correas trapeciales aconseja no utilizarlas para velocidades lineales mayores de 25 m/s, pues, aunque se sabe la velocidad lineal incide notablemente en la potencia a transmitir, la fuerza centrífuga reduce el contacto correa-polea y limita la capacidad de transmisión de potencia.
La velocidad se puede variar eligiendo de forma adecuada el diámetro de la polea, si bien condiciones variadas de montaje o de diseño pueden obligar a usar transmisiones con correas múltiples.
Antes de finalizar este apartado se van a enumerar una serie de ventajas e inconvenientes que presentan las correas trapeciales.
Entre las ventajas se pueden enunciar:
- La distancia entre ejes puede ser tan pequeña como permitan las poleas.
- La relación de diámetros entre poleas puede ser muy grande, llegando hasta 12/1.
- Las correas trapeciales trabajan en cualquier posición.
- Pueden usarse correas múltiples.
- Requieren gracias al efecto cuña muy poca tensión inicial.
- Soporta muy bien las temperaturas extremas.
- No atacan a los cojinetes de soporte de las poleas por tensión excesiva.
- Resisten la intemperie.
- Hay modelos especiales SPA, SPB... que soportan condiciones muy adversas y agresivas.
Entre los inconvenientes es preciso tener en cuenta que:
- Las grasas, aceites, gasolinas y gas-oil las atacan.
- Su longitud crece con el uso.
- El deslizamiento las destruye rápidamente.
Para concluir indicar que las correas trapeciales deben trabajar siempre en un plano, si
bien hay ocasiones en las que pueden montarse con transmisiones tan diversas que resulta hasta espectacular.
POTENCIA TRANSMITIDA POR UNA CORREA
La potencia transmitida por una correa es función de la diferencia entre las tensiones de sus ramas y de su velocidad lineal, ya que como se observa en la siguiente figura, el par transmitido viene dado por:
Siendo:
M = par motor.
F1 = fuerza en el ramal más cargado.
F2 = fuerza en el ramal menos cargado.
r = radio de la polea.
Y como entre las expresiones de la potencia se tiene que:
N = M• n
Siendo:
N = potencia.
M = par motor.
n = régimen de giro.
Sustituyendo la primera expresión en la segunda se tiene:
N = (F1 − F2 )• n • r
Y como:
n·r = velocidad lineal de la correa se tiene:
N = (F1 − F2 )• v
Siendo:
N = potencia transmitida.
F1 - F2 = diferencia de carga entre los ramales de la correa
v = velocidad lineal de la correa.
El cálculo de instalaciones de transmisión de potencia con correas trapeciales podría hacerse con una metodología semejante a la desarrollada. Hoy, la amplia oferta comercial existente ofrece al técnico tablas y ábacos que permiten un cálculo rápido y preciso de este tipo de transmisiones. De esta forma la tabla siguiente aporta la potencia teórica que puede transmitir una correa en función de su velocidad lineal, trabajando en condiciones normales.
Cuando las condiciones son adversas se aplica la fórmula empírica:
Nreal = ( Nteorica.C1.C3 ) / C2
Siendo:
C1 = coeficiente de corrección del ángulo de contacto correa-polea
C2 = coeficiente de corrección debido a sobrecargas en la transmisión
C3 = coeficiente de corrección debido a la utilización de diámetros menores que los mínimos permisibles.
diámetro de uso elegido
C3 = _____________________________________________
diámetro mínimo aconsejado por la norma UNE 18164
La tabla siguiente ofrece los valores de C1 según el ángulo de contacto.
El coeficiente de corrección de sobrecargas se ofrece en sendas tablas.
La tabla siguiente ofrece los valores de C2 en función del % de sobrecarga y la tabla 8 ofrece C2 en función del tipo de la transmisión.
El número de correas precisas para cada instalación se calcula dividiendo la potencia necesaria entre la potencia transmitida por cada correa con el método de cálculo hasta aquí
expuesto.
El ábaco siguiente es un prontuario indicativo de las condiciones óptimas de utilización de cada tipo de correa.
CORREAS DENTADAS. CARACTERÍSTICAS Y CÁLCULO
Constituyen las correas dentadas un sistema moderno de transmisión de potencia que reúne la práctica totalidad de los ventajas de las correas planas y trapeciales y elimina sus inconvenientes. Entre los nombres con los que se comercializan se les llama correas de sincronización que es bastante definitorio de una de sus más importantes cualidades. Sus elementos de tracción usuales son cables de acero y es por lo que estiran muy poco bajo carga y servicio y soportan grandes esfuerzos. Su tensión inicial puede ser muy baja, lo que origina una reducida carga en los cojinetes y no precisa (aunque no son desechables) elementos tensores.
Se construyen a base de neopreno al que se le coloca una cubierta exterior de nylon. Como las poleas que requieren se tallan con dientes la transmisión que realizan es sincronizada lo que en muchos casos además de útil es necesario. Tienen un funcionamiento silencioso, no
precisan lubricación. Para su cálculo es preciso tener en cuenta que, según indica la experiencia, debe haber un mínimo de seis dientes en contacto.
La relación de transmisión de estas correas viene dada por la expresión:
dp1 ⋅n 1 = dp2 ⋅n 2
Siendo:
dp1 y dp2 los diámetros primitivos de las poleas
n1 y n2 el número de revoluciones de ambas poleas.
Por una fórmula básica en engranajes se tiene que:
π ⋅dp1 = p ⋅ Z1
Siendo:
p = paso
Z1 = nº de dientes de la polea 1
Despejando en la ecuación anterior se tiene:
dp1 = (p*Z1)/ π
Y llamando módulo a:
m=p/π
Como:
p/π=dp1/Z1=dp2/Z2
Se tiene que:
dp1 = m.Z1
Y por tanto:
dp2 =m.Z2
Sustituyendo dp1 y dp2 se tiene que la relación de transmisión también puede expresarse por:
Z1⋅n1 = Z2 • n2
El número mínimo de dientes en contacto entre la polea más pequeña y la correa se calcula por la fórmula:
Zc =(β.Z1)/360
Ecuación en la que:
Zc = número de dientes en contacto.
β = ángulo de contacto polea-correa.
Z1 = número de dientes de la polea.
En este tipo de correas se denomina Potencia base a la potencia transmitida por cada cm de anchura de correa.
Estas correas se agrupan comercialmente en los tipos XL, L, H, XH, y XXH.
Sus características de paso se presentan en la siguiente tabla.
Los fabricantes ofrecen catálogos en los que aportan la potencia base de los distintos modelos de correas. En la tabla siguiente se presenta la potencia base de una correa del tipo L para diferentes valores del diámetro primitivo y para diferentes regímenes de giro de la polea más pequeña usada en la transmisión.
La potencia de cálculo o potencia corregida Pc se obtiene afectando a la potencia a transmitir (P) de los correspondientes coeficientes de corrección según la fórmula:
Pc =P• (C1 +C2 +C3 )
Siendo:
C1 = coeficiente de corrección debido a sobrecargas en la transmisión.
C2 = coeficiente de corrección debido a la multiplicación y se obtiene según el número de dientes de contacto de la correa con las poleas.
Si Z1 es el número de dientes de la polea motora y Z2 es el número de dientes de la polea
arrastrada
Si Z1/Z2 ≤ 1 ⇒ C2=0
Si Z1/Z2 > 1 se asigna a C2 el valor ofrecido por la tabla 12.
Pc =P• (C1 +C2 +C3 )
Siendo:
C1 = coeficiente de corrección debido a sobrecargas en la transmisión.
C2 = coeficiente de corrección debido a la multiplicación y se obtiene según el número de dientes de contacto de la correa con las poleas.
Si Z1 es el número de dientes de la polea motora y Z2 es el número de dientes de la polea
arrastrada
Si Z1/Z2 ≤ 1 ⇒ C2=0
Si Z1/Z2 > 1 se asigna a C2 el valor ofrecido por la tabla 12.
C3 = coeficiente de corrección debido al tiempo continuado de funcionamiento.
Este coeficiente se obtiene de la tabla 11.
La tabla siguiente ofrece los valores de C1 según el tipo de instalación en la que se apliquen correas dentadas.
Este coeficiente se obtiene de la tabla 11.
La tabla siguiente ofrece los valores de C1 según el tipo de instalación en la que se apliquen correas dentadas.
La tabla siguiente ofrece los valores de C2 y C3.
Una vez conocida la potencia corregida Pc y la potencia base que puede transmitir una determinada correa Pb se obtiene la anchura de correa necesaria por el cociente de ambas, o sea:
Una vez calculado b se escoge en catálogo el ancho comercial inmediatamente superior. Los anchos comerciales de las correas dentadas son los que se presentan en las siguientes tablas.
Las poleas que se usan para transmisiones con correas se fabrican con distintos materiales, siendo los más comunes fundición de hierro, acero y aleaciones ligeras. A veces se encuentran poleas de madera (muy antiguas) y de plástico. Hoy las dimensiones de las poleas están normalizadas.
Las poleas para correas planas se construyen con llanta (superficie de contacto correa-polea) plana o ligeramente abombada según se presenta en la figura siguiente. El objeto de esta conformación es el de estabilizar la correa evitando con ello que se salga por el lateral.
Una vez conocida la potencia corregida Pc y la potencia base que puede transmitir una determinada correa Pb se obtiene la anchura de correa necesaria por el cociente de ambas, o sea:
Una vez calculado b se escoge en catálogo el ancho comercial inmediatamente superior. Los anchos comerciales de las correas dentadas son los que se presentan en las siguientes tablas.
POLEAS
Las poleas para correas planas se construyen con llanta (superficie de contacto correa-polea) plana o ligeramente abombada según se presenta en la figura siguiente. El objeto de esta conformación es el de estabilizar la correa evitando con ello que se salga por el lateral.
La flecha h tiene una dimensión de 1/3 √b a 1/2√b
La fijación de las poleas a los árboles se realiza mediante chavetas, o mediante el denominado cubo partido, elemento de gran utilidad cuyo esquema es el representado en la figura siguiente.
El funcionamiento del cubo partido es tan simple como apretar la placa de fijación contra la polea mediante tornillos. En la polea se ha conformado previamente un contracono en el que ajusta el cubo partido. Las poleas para correas trapeciales son acanaladas y cuando son pequeñas se construyen de una sola pieza, en cambio para grandes transmisiones es frecuente usar varias poleas unidas mediante tornillos.
Las características dimensionales de estas poleas están normalizadas y, para los distintos tipos de correas, ya han sido presentadas. Es importante destacar que el acabado de los caras laterales debe ser lo más fino y uniforme posible para evitar el prematuro desgaste por
abrasión.
Las poleas para correas dentadas parecen engranajes de gran paso. Para un funcionamiento continuado y sin problemas es muy importante que las aristas de los dientes se redondeen.
La figura siguiente presenta un detalle de una polea dentada con su correa.



























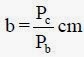








ResponderBorrarHola que tal es acerco información sobre un fabricante de correas industriales a muy buen precio espero les sirva.
Correas Dentadas, Correas Industriales, Correas Planas - Tisa Transmisiones
Fabrica de Correas. Nos dedicamos a la venta de Correas Planas, Correas dentadas, Correas de transmision, Correas trapeciales, Correas industriales.
http://tisatransmisiones.com.ar/correas-industriales.html
Tags: correas dentadas, correas industriales, correas planas, correas industriales precios
Necesito banda o correa dentada de 3/8" de paso con un ancho de 1/2" y con 72 dientes en una longitud de 27", la atura total de 1/8" y altura de diente 1/16".
ResponderBorrarLa direccion
ResponderBorrarPorfavor